Tackling Exploration-Exploitation Dilemma in K-armed Bandits
Briefing About two methods, Epsilon Greedies and Thompson Sampling with implementations in python

In real world, we came across many situations where we face a well-known tradeoff of Exploration and Exploitation. But what do we mean by these terms?
Exploitation is the process of taking benefits from things which we know about and Exploration is to get knowledge about things which we didn’t know.
I will try to explain these terms with one example, Suppose you like mathematics and always given preference to it’s topic compare to any other subject. Now in this situation, you always favor (exploit) mathematics because it provided you great returns in the past. But only choosing mathematics not allow you to explore other subjects. So just for experimentation, you have randomly chosen chemistry(Exploration) and found some interesting topics. Hence, your selection allowed you to know more about other things. But the tradeoff is that you cannot study mathematics and chemistry simultaneously. This is the dilemma of Exploration-Exploitation we are discussing.
To see this in action, we are considering the simplest setting from Reinforcement learning, i.e., MultiArmed Bandits. It’s like a slot machine in which every time you pull the arm it will generate a reward depicting how favorable the particular action and move to a terminal state.
Before Getting into the Actual methods, let me briefly discuss some of the terminologies extensively used in the literature of RL and bandits.
DEFINITIONS
- Rewards- It can be defined as the benefit or comfort.
- Actions- In the case of a bandit problem pulling an arm is defined as the Action.
- Action-Values - It defines the quality of Action a taken by an Agent in a state s. But for bandits, since every action leads to a terminal state it can be thought of as a single state problem and only depend on actions. Mathematically,
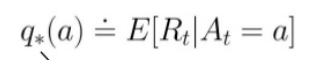
It is a blessing in disguise if we know about the optimal q values for each action. But in reality, we didn’t know about it, but rather we estimate these values based on the experiences we collected by pulling arms successively. One such method is Sample Averaging defined as,

For sufficiently large samples, it approaches to true Q* (by central limit theorem). Still, we need to balance exploration and exploitation for guaranteed convergence of each action to its optimal value. We will deal with two methods for this in the next section.
Why These two methods, and not others?
Before moving further, one question may arise that there are different other methods for tackling this dilemma like epsilon Greedies, Upper Confidence Bound, Optimistic Initial Values, then why chosen these two. The answer is that I am trying to provide a lower and upper bound on these, as epsilons are generally the starting point for dealing with these tradeoffs and Thompson Sampling has got its name recently as one of the state of the art in this.
Environmental Settings
For comparing this solution, I simulated the 10 Armed TestBed Same as Described in Sutton And Barto Book i.e., by sampling Q* from standard normal distributions and then rewards sampling from gaussian with means Q* and variance 1. True Reward Distribution is shown as:

Class of Epsilon Greedies
Epsilon Greedies are a class of Algorithms with only a change of parameter epsilon that accounts for exploration. If epsilon = 0 means pure Greedy and any other epsilon between 0 and 1 implies some exploration. The main notion of these algorithms is that instead of taking greedy actions every time instead choose an action randomly from other actions uniformly with probability epsilon.
Thompson Sampling (a.k.a. TS)
Thompson sampling is based on the notion of Bayesian Inference in which we update our beliefs about the parameters(known as priors) with the data we observed (known as posterior probability). To know more about these terminologies, checkout the blog post below.

Now, After knowing the posterior distribution, what Thompson sampling does is that it samples the actions from these posterior distributions. Hence, if an action is less explored, its chances are more to be picked. After a sufficient timestep, i.e., when each action is sampled enough times, it will analyze final distributions to get optimal action and start exploiting it afterward. In doing so, it utilizes a perfect method of Conjugate priors to reduce complexity. I am focussing on the core implementation here, hence for knowing the detailed theory visit this reference on TS
Algorithms and Implementations
For Comparison between Eps-Greedy and TS, I modified the algorithm of normal epsilon greedy to create the same set of conditions so that the whole focus is on the actual core part that is the difference between sampling from model(in TS) to taking estimate from model( mode/mean in Eps-Greedy). I also made the algorithm by myself in latex for more realistic Gaussian Sampling with assuming(variance = 1).


The last two lines show the parameter updates which utilize the conjugate priors property. These algorithms will be clear from the code.
In the above code, I made a class Bandit to simulate the properties of a single bandit and a class to keep track of logs collected over time. Now let’s move to the two Algorithms implementation.
In the above code, we used the same methodologies discussed previously. All the things are same in both cases except the _choose_bandit function as described in algos.
Results
We plotted the Excepted_Rewards for each method for 1500 timesteps on 2500 independent simulation runs and took its average.

From the above plot, it can be inferred that from all the eps-Greedies eps= 0.01 can be considered best as it is increasing not plateaus but even this one is very low wrt to Thompson Sampling. Now to investigate further, we plot the Average percentage of Optimal Action over all independent runs for eps = 0.01 and TS to see the superiority of TS.

Nice!! From the above plot, we can conclude that even both methods favoring action-2 but still eps = 0.01 hardly reach 80% even in later stages but TS gave optimal action with 100 % even in the early period. It shows that TS quickly explored all actions and then exploiting the optimal one.
Conclusion
After going through the article, one can have two questions in mind. Firstly, true rewards sampled from Gaussian and prior used as Gaussian is it good? and secondly, considered variance is fixed. So, the answer is, that I used a minimal implementation of Gaussian TS, with variance fixed but it is pretty easy to do without knowing any assumption on variance. Assuming Gaussian as priors not harm because we know that most natural phenomena follow it and every distribution approaches Gaussian for large samples( central limit theorem), hence there is no lack of generality and we can see that TS outperformed epsilon Greedies. If you liked my article feel free to upvote this article and you can found the entire code on my repo here- https://github.com/Amshra267/Thompson-Greedy-Comparison-for-MultiArmed-Bandits

